Projects > Codility Problems

Here is another project to improve my programming skills. Codility is a software company that specializes in code testing. That is, they provide problems for which you have to write code to solve, after you submit your code, they analyze it and grade it for you.

Currently they have three demo exercise which can be attempted by anyone. There are also monthly coding challenges that are quite difficult but reward the person who can solve the challenge flawlessly with a certificate. I will attempt those too and post the certificates when i get them!

Please note that the main reason I am doing this is to learn! If you find any mistake in my solution, please don't hesitate to contact me.

I will solve the problems in more than one programming language, initially though, i will start with Python 3. Furthermore, i will post the evaluation report provided by Codility for each.

Please choose the problem from the box below:

Problem Description:

Demo test on Codility

Given an array A of N integers, we draw N discs in a 2D plane such that the I-th disc is centered on (0,I) and has a radius of A[I]. We say that the J-th disc and K-th disc intersect if J ≠ K and J-th and K-th discs have at least one common point.

Write a function:

def solution(A)

that, given an array A describing N discs as explained above, returns the number of pairs of intersecting discs. For example, given N=6 and:

	A[0] = 1  A[1] = 5  A[2] = 2
	A[3] = 1  A[4] = 4  A[5] = 0

intersecting discs appear in eleven pairs of elements:

• 0 and 1,
• 0 and 2,
• 0 and 4,
• 1 and 2,
• 1 and 3,
• 1 and 4,
• 1 and 5,
• 2 and 3,
• 2 and 4,
• 3 and 4,
• 4 and 5,

So the function should return 11.

The function should return −1 if the number of intersecting pairs exceeds 10,000,000.

Assume that:

• N is an integer within the range [0..100,000].
• each element of array A is an integer within the range [0..2147483647].

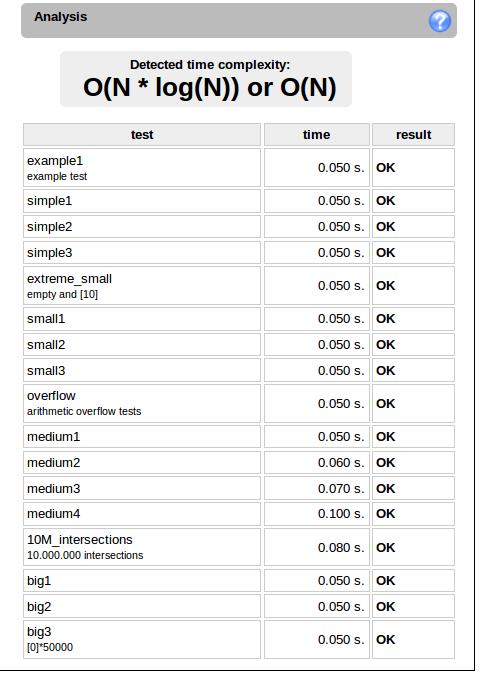
Complexity:

• expected worst-case time complexity is O(N*log(N))
• expected worst-case space complexity is O(N), beyond input storage (not counting the storage required for input arguments).

Elements of input arrays can be modified.

Code:

• Python

from bisect import bisect_right
 
def solution(A):
    """Finds number of disk intersections in a 2D plane
 
    Given an array A where its indices represent circles and the array values
    represent the radius of the circle, returns the number of pairs of
    intersecting discs.
 
    """
 
    #Variable to track number of intersections found
    intersections = 0
 
    #Create intervals list. This is basically a list of tuples where each tuple
    #contains the lowest point in the circle along the y-axis, and its
    #corrosponding highest point. For example, entry with index 0 and
    #radius 3 will have an interval from -3 to +3, stored as (-3, 3).
    intervals = sorted( [(i-A[i], i+A[i]) for i in range(len(A))] )
 
    #Now we filter all the starting points of each interval entry and store
    #them in this array. So for intervals (-3, 3), (1, 4), and (5, 6); create
    #a list containing -3, 1, and 5.
    starts = [i[0] for i in intervals]
 
 
 
    for i in range( len(starts) ):
 
        #This is where the magic happens. Now, we look at the ending point of
        #each interval, that is the 6 in a tuple like (1, 6). Then we attempt
        #to insert it into the list starts. Keeping in mind that the list
        #starts is sorted, the position at which the ending point is
        #inserted indicates the number of points its circle intersects with!
        intersections_temp = bisect_right(starts, intervals[i][1])
 
        #Subtract current position from intersections found as this will
        #exclude duplicate intersection points. That is points like (1,3) and
        # (3, 1) only count once. Also, subtract one unit to exclude self
        #intersections. That is points like (3, 3) don't count.
        intersections_temp -= (i+1)
 
         
        #Add the intersections found for circle i to the total itnersections
        #count
        intersections += count
 
        #Special case for Codility tests, terminate if too many intersections
        #are being processed.
        if intersections > 10000000:
            return -1
 
    return intersections
    

Codility Evaluation: